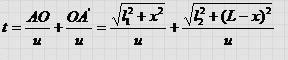|
|
|
|
Принцип Ферма
Принцип минимального времени
В 1660 г. П. Ферма, сформулировал принцип, который явился обобщенным законом и геометрической оптики. В простейшей формулировке этот принцип звучит так.
В вакууме скорость света максимальна. В оптической среде с показателем преломления п время прохождения светом того же расстояния увеличивается в п раз. Величина s, равная пpoизведению абсолютного показателя преломления n на пройденном расстояние l (s = nl), называется оптической длиной пути. Принцип Ферма относится именно к оптической длине пути
Прямолинейность распространения света.
Используя принцип Ферма, можно получить закон прямолинейного распространении света. Свет из одной точки в другую распространяется по кратчайшему расстоянию. В однородной среде кратчайшим оптически и путем является прямая линия.
Однако в неоднородной среде кратчайшим оптическим путем может оказаться некоторая кривая (или ломаная) линия, вдоль которой показатель преломления меньше, чем вдоль геометрической прямой. Этим объясняется явление преломления света и искривление световых лучей в неоднородной среде — явление рефракции.
Закон отражения.
|
Пусть на зеркальную поверхность падает свет из точки А. В точке А' собираются лучи, отраженные от зеркала. Предположим, что свет из точки А в точку А' может распространяться двумя путями — отражаясь от точек О и О'. Время, которое потребуется свету, чтобы пройти из источника А в точку А' через точку О, можно определить из выражения
Здесь u — скорость распространения света. Покажем, что время прохождения света по траектории АОА' меньше, чем по любой другой траектории АО'А'. Продифференцируем выражение и приравняем производную нулю в соответствии с принципом Ферма. |
Учтем, что sin a = x/AO, sin a’ = (L - х) /ОА'. Получим:
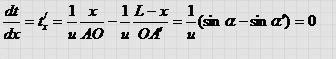
Отсюда получаем sin a = sin a '; а так как оба угла острые, то отсюда следует равенство углов:
a = a '
Мы получили соотношение, выражающее закон отражения угол отражения a' равен углу падения a . Из принципа Ферма следует и вторая часть этого закона: отраженный луч
лежит в плоскости, проходящей через падающий луч и нормаль сражающей поверхности. Ведь если бы эти лучи лежали в разных плоскостях, то не был бы минимальным путь АОА'.Закон преломления света
|
|
Закон преломления света. Аналогичным образом, используя принцип Ферма, рассмотрим явление, происходящее на границе раздела двух сред. Пусть в среде I скорость света u1, в среде II — u2. Для прохождения света из точки А1 в точку A2 будет затрачено время
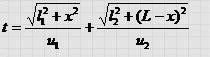
Выберем из всех возможных траекторий распространения света ту, которой соответствует минимальное время распространения света. Продифференцировав и положив производную равной пулю, получим:
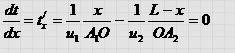
Учитывая, что sin a1 = x/A1O, sin a2 = (L - х) /ОА2 получим :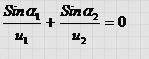
Откуда следует :
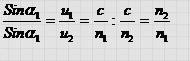
Это и есть закон преломления света. Запишем его в более удобной форме.
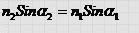
Из построений и принципа Ферма следует также, что преломленный луч лежит в плоскости, проходящей через падающий луч и перпендикуляр к поверхности раздела двух сред.
Рассматривая падение светового пучка на границу раздела двух сред, мы говорили раздельно об отражении и преломлении света. Это было вызвано необходимостью вывода законов отражения и преломления света. Однако практически всегда на границе раздела двух сред световой пучок разделяется на два - отраженный и преломленный.
